Publications

2024

1. 

   Spectral analysis of representational similarity with limited neurons

   Hyunmo Kang, Abdulkadir Canatar, and Sueyeon Chung

   2024

   Abs PDF

   Understanding how neural representations align between biological and artificial systems has emerged as a central challenge in computational neuroscience. While deep neural networks now reliably predict neural responses across multiple brain areas, their utility for understanding biological computation remains limited by our ability to accurately measure representational similarities. This limitation becomes particularly acute when working with sparse neural recordings, where traditional similarity metrics may fail to capture true representational relationships. Recent spectral analyses of similarity measures provided careful decomposition of neural similarities in the regime of small sample sizes. Here, we consider Centered Kernel Alignment (CKA) as a similarity measure and, using techniques from random matrix theory, identify what spectral aspects affect the representational similarity in the limited neuron regime. We show that the true CKA is underestimated when a small population of neurons is randomly sampled and compared with deterministic neural network representations. We find that increasing sample size may cause underestimating the true CKA. When the number of neurons is small, we demonstrate that only information up to a certain eigenvector threshold can be resolved. We develop a systematic method to denoise the CKA and demonstrate a similarity measure that is robust against changes in population size.

2. 

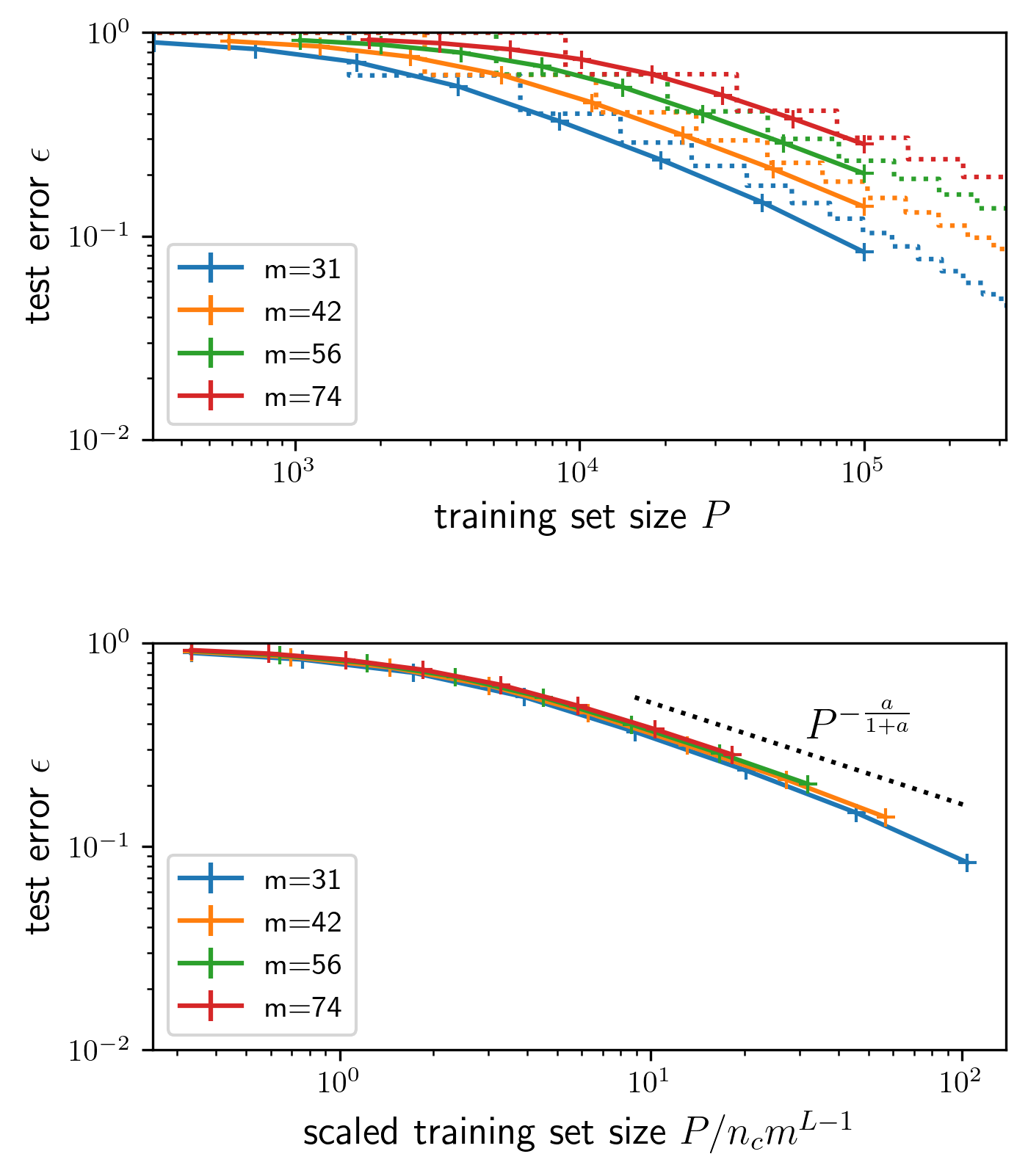   How rare events shape the learning curves of hierarchical data

   Hyunmo Kang, Francesco Cagnetta, and Matthieu Wyart

   2024

   Abs PDF

   The learning curves of deep learning methods often behave as a power of the dataset size. The theoretical understanding of the corresponding exponent yields fundamental insights about the learning problem. However, it is still limited to extremely simple datasets and idealised learning scenarios, such as the lazy regime where the network acts as a kernel method. Recent works study how deep networks learn synthetic classification tasks generated by probabilistic context-free grammars: generative processes which model the hierarchical and compositional structure of language and images. Previous studies assumed composition rules to be equally likely, leading to non-power-law behavior for classification. In realistic dataset, instead, some rules may be much rarer than others. By assuming that the probabilities of these rules follow a Zipf law with exponent a, we show that the classification performance of deep neural networks decays as a power a/(1+a) of the number of training examples, with a large multiplicative constant that depends on the hierarchical structure of the data.